追加
倍率は,光学系によって生じる像の大きさの物体の大きさに対する比で表す.
◎レンズによる像のでき方は,
a)焦点とレンズとの間
b)焦点の位置
c)焦点より外で有限
d)無限遠(∞)
がある.結像の基本は 平行光線= ∞ であるが,すべて作図で計算できる.
拡大率は,実際の物体の大きさに対する虚像の大きさとなる.これにより,
見ている人の屈折状態(屈折異常の矯正や老視の有無)やレンズの位置に左右されることになる.
◎拡大・縮小の考え方は,
ⅰ)レンズの結像を作図・計算
ⅱ)拡大鏡としての distance magnification
ⅲ)眼鏡レンズとしての spactacle magnification
がある.
●倍率 magnification その一
物体及び像の大きさを,光軸に垂直な直線上の長さをとったものを横倍率 linear magnification ,光軸上に沿った長さをとったものを縦倍率 axial magnification と言う.
通常,倍率は横倍率のことをを指す.
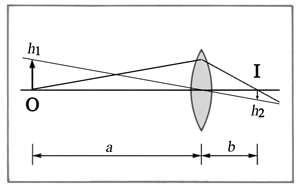
㈠:物点OはPジオプトリのレンズを通して像点Iに結像する.
このとき,
U + P = V
倍率 m は,
m = U/V = U/(U+P)
なお,符号「+」は正立像を示す.
m <1で縮小,
m >1で拡大となる.ただし,
U(ジオプトリ)=レンズを通る時の物体の光の広がり(object vergence),すなわち物体Oとレンズとの距離 a
P(ジオプトリ)=レンズの屈折力(vergence-change),
V(ジオプトリ)=結像点での光の広がり(image vergence),すなわちレンズと結像点Iとの距離 b
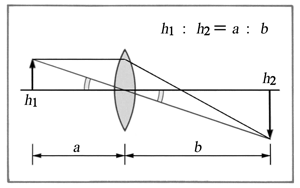
㈡:レンズから有限の位置にある時,物点Oの高さと像点Iの高さはレンズ(の節点N)からのそれぞれの距離と比例関係にある(相似三角形).
OとIまでの距離をそれぞれ a と b とすると,
倍率 m は,h2/h1 であるから,
m = h2/h1 = b / a ・・・・・・ (1)
焦点距離 f のとき,a:b = f:b-f であるから,
| 1 | + | 1 | = | 1 |
・・・・・・ (2) |
| ― | ― | ― |
| a | b | f |
㈢:凸レンズをルーペとしての使用では,物側焦点(F1)よりレンズに近づいた位置に対象(O)がある.
このときのOと虚像(I)までの距離をそれぞれaとbとして,上と同じように倍率は,
m = b / a ・・・・・・ (1)
問題は,虚像(I)の位置である.
焦点距離 f に対して,a:b = f:b+f であるから,
| 1 | = | 1 | - | 1 |
・・・・・・ (2') |
| ― | ― | ― |
| f | b | a |
∴
| b = |
a・f |
・・・・・・ (2”) |
| ――――――― |
| f - a |
または,
| b | = | f | = | 1 | = 1 - |
b |
・・・・・・ (3) |
| ― | ―――――――― | ―――――――― | ― |
| a | f - a | 1 - a/f | f |
光線の進行方向を正として,a bは正負のいずれかになる.倍率の正負は像の正立と倒立に対応する.
式(1)は絶対値となる(
m =|b/a|).
☆例えば
① レンズの前(a=) 1 m(左側つまり U=-1 )にある物体Oの像は,+4Dレンズを通過すると後ろ(b=)0.33 m(右側つまり V=+3 )に結像する場合では,
m = -1/-1+4 = -1/3
符号「-」は倒立像で,サイズは 3分の1 であることを示す.
すなわち,33%の大きさの倒(実)像である.
② 焦点距離 50 mm の凸レンズに対し,レンズの前 150 mm のところにある物体の像の位置と大きさは?
a=150mm,f=50mm により,
| 1 | + | 1 | = |
1 |
∴ b = |
150 |
= 75(mm) |
| ――― | ― | ―― | ――― |
| 150 | b | 50 | 2 |
| m = | b | = |
150 |
・ |
1 |
= |
1 |
= 0.5(倍) |
| ― | ――― | ――― | ― |
| a |
2 | 150 | 2 |
これによりレンズから 75 mm の位置に 0.5 倍の像を作る(実像 上記㈡.
③ 焦点距離 50 mm の凸レンズに対し,レンズの前 25 mm のところにある物体の像の位置と大きさは?
a=25mm,f=50mm により,
| 1 | + | 1 | = |
1 |
∴ b = -50(mm) |
| ―― | ― | ―― |
| 25 | b | 50 |
| m = | b | = | (-50 )・ | 1 |
= -2(倍) |
| ― | ―― |
| a | 25 |
これによりレンズの前 50 mm の位置に 2 倍の像を作る(虚像 上記㈢.
符号「-」は物体側に虚像ができることを示している.
④ +5Dのレンズでは,レンズから10cm 離れた対象は 20cm のところに(2倍に拡大された)虚像を生じる.
⑤ 焦点距離 50 mm の凹レンズに対し,レンズの前 100 mm のところにある物体の像の位置と大きさは?
a=100mm,f=-50mm により,
| 1 | + | 1 | = - |
1 |
∴ b = - |
100 |
= - 33.3(mm) |
| ――― | ― | ―― | ――― |
| 100 | b | 50 | 3 |
| m = | b | = | (- | 100 | )・ | 1 | = - | 1 | = -0.33(倍) |
| ― | ――― | ――― | ― |
| a | 3 | 100 | 3 |
これによりレンズの前 33.3 mm の位置に 0.33 倍の像を作る(虚像).
㈣:無限遠にある物体では,
物体の視角 θ と焦点距離 f により,像の大きさ I= f・tan θ ・・・・・ (4)
●拡大率 magnification その二
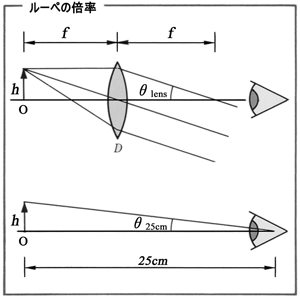
光学機器を通じて観察した物体の見掛けの大きさと機器なしで見た大きさ(視角)の比を角倍率 angular magnification と言う.我々が「虫めがね・拡大鏡・ルーペ loupe/Lupe 」を用いる場合,角倍率変換による拡大効果を利用している.これは,焦点距離の短い凸レンズによって対象の拡大した虚像を作り,目視観察する.
拡大率は対象やレンズの位置,眼の屈折状態で変化する.ルーペの使い方として次のような状況を想定する.
○ 対象をレンズの物側焦点に置く.レンズを通った光線は平行となるので虚像は ∞ にある.
○ 虚像の位置が眼前 25cm になるように対象を置き,眼をレンズに近づけて虚像を見る.
○ 眼を像側焦点に置く.
観察像はみかけの大きさ,つまり相対的なものであるから,比較するための基準が必要である.慣習上,参照距離(作業距離)を「25cm 」に決め,これを1倍とする.明視するためには,像点が明視域あるいは調節域の中になければならないことで,正視裸眼(且つ,4D以上の調節力がある状態)を前提としている.そのようなことで,商品としての拡大鏡の倍率表記は一定していない.
㈠:焦点の位置に対象を置くことで,レンズを通したのち平行光線となるため観察眼とレンズの距離に関係なく一定の拡大率となる(虚像は ∞,正視眼の遠点).
倍率 m = 物体との距離/f
焦点距離 f m のレンズを使用したときの視角 θlens = tan-1(h/f m),
25cm 離れた対象の高さ h m の視角 θ25cm = tan-1(h/0.25 m)
これにより
| 倍率 m = |
tanθlens |
≒ |
θlens |
= |
D |
・・・・・ (5) |
| ―――――― |
――――― |
― |
| tanθ25cm |
θ25cm |
4 |
実際にはレンズ度(D)だけで拡大率が決まるわけではないらしい.
㈡:「25cm 」に決めた距離に像を作るためには,式(3)より,
b = -0.25 ,D = 1/f
∴
| 倍率 m = | b | = 1 + |
D |
・・・・・ (3') |
| ― | ― |
| a | 4 |
㈢:凸レンズを眼に付けた状態では,レンズのよる像の拡大ではなく視距離を変えることになる.見ようとする物体は,近づくほど網膜の像(視角)が大きくなる.距離が半分になれば網膜像は2倍に写る.この場合の参照距離は「40cm」と決められている.すなわち,物体が眼前「40cm」にあるときの網膜像が1倍である.この場合の観察眼は「+2.5D 」を付加した状態と同等になっている.これを「+10D 」とすると眼前「10cm」であるから,4倍となる.
◎tan-1 または arctangent は
tan θ = l を変形して tan-1 l = θ
◎実際のルーペの拡大率は・・・‥
このように対応
●拡大率 magnification その三 【~眼鏡倍率:屈折異常 refractive error を矯正する場合,網膜に映る像の拡大・縮小が問題となる.これが眼鏡倍率である.
① 眼鏡倍率 SM:spectacle magnification
裸眼での網膜像の大きさに対する矯正時の網膜像の比率のことで,spectacle magnification=power factor×shape factor で表わす.
通常では,遠用眼鏡に適応する.
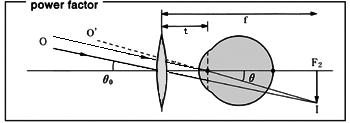
a.power factor
これは倍率(一)の計算があてはまる.右図は遠視眼での作図例である.
考え方は,
充分に遠方にある物体 O は,厚みを無視した焦点距離 f(Dジオプトリ)のレンズにより遠視眼の遠点F2 に結像する.このときの像の大きさ I は,
I=f・tan θ0
この像は見ている眼よりも前(=物体側)にあるレンズ系によるものである.
一方,眼から見ると物体 O’がF2 に結像していることを示す.眼球のレンズ系(=像側)では像 I と物体 O’とは共役関係にあるという意味である.このときの像の大きさ I は,
I=(f-t)・tan θであるから,
| 拡大率 m = |
θ |
= |
f |
= |
1 |
= |
1 |
・・・・・ (6) |
| ―― | ―――― | ―――――― | ―――――――― |
| θ0 | f-t | 1 -t/f | 1 -t・D |
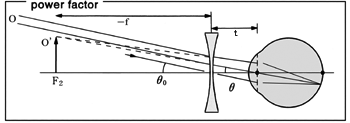
近視眼では,
凹レンズは近視眼の遠点F2 に O’として像を作る.このときの像の大きさ I は,
I=-f・tan θ0
これは視角θの物体として見える.このとき
| tan θ = |
I |
であるから, |
| ――――――― |
| -f +t |
| 拡大率 m = | tanθ | = | -f |
| ――――― | ――――――― |
| tanθ0 |
-(f-t) |
ということで,式(6)が成り立つ. |
b.shape factor
レンズの中心厚を考慮した係数.
| sf = | 1 |
| ―――――――――― |
| 1 -C・D1 |
これにより拡大率は,
| SM = sf・ |
1 |
( t はレンズ頂点から入射瞳までの距離,D は頂点屈折力 |
| ―――――――― |
| 1 -t・D |
c.頂間距離について
ここで両レンズ系間の距離,すなわち「 t 」が重要となる.眼鏡レンズは 15mmとして設計されている.眼内ぶんは 3mmであるので,実際の眼鏡レンズでは角膜から 12mmの位置にある.これが頂間距離である.コンタクトレンズの頂間距離は0mmであるので,ある程度以上では眼鏡レンズとコンタクトレンズで度数のずれは大きくなる.
(本当の度数はどっち ?
② 相対眼鏡倍率 RSM:relative spectacle magnification
標準正視眼での網膜像の大きさに対する矯正時の網膜像の比率のことで,これにより軸性屈折異常と屈折性屈折異常の差が解釈できる.
| RSM= |
1 |
(t は頂間距離,D はレンズの屈折力 |
| ―――――――― |
| 1+t・D |
一般に前焦点以内に眼鏡があるので(前焦点にレンズの主点が一致した時,網膜像は正視の場合に等しい),
屈折性屈折異常では,近視の場合は正視より小,遠視は大である.
軸性屈折異常では,近視の場合は正視より大,遠視は小である.
③近用眼鏡の倍率
・・・

◎近軸光線
光軸からあまり離れることなく,傾角もあまり大きくならない光線.無収差レンズとも見做せる.
数学的には sin をラジアンで,tan を θ で代用できる.(cosは1 ?)
◎入射瞳 その1
入射瞳(にゅうしゃひとみ entrance pupil)は,光量絞りより左側にあるレンズ系による像.言い換えると物体側より見た絞の虚像で,すべての有効光はこの絞りに入射する.絞り(開口絞り)は光線束を制限しているので明るさが低下する.
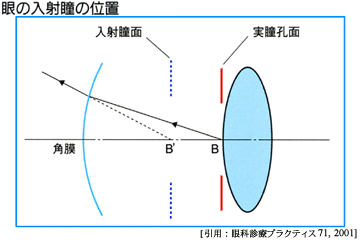
◎入射瞳 その2
眼の入射瞳は,実瞳孔の角膜屈折による虚像になっている.
角膜を薄いレンズと仮定しその屈折力を K(D),角膜前面から実瞳孔までの距離を s,眼内(房水)屈折率を n とすると,入射瞳までの距離 s' は,s'=s/(n+sK)となる.入射瞳の倍率(拡大率)は,M=ns'/s である.ここで,
s=-3.60×10-3 m,n=1.336とし,K=45D の時,s'=-3.07×10-3 m,M=1.14となり,0.5mmほど浮き上がって,14%ほど拡大されて観察される.
眼科臨床で測定されている瞳孔径は,厳密には入射瞳径である.屈折矯正手術で K が小さくなると瞳孔の拡大量が少なくなる.角膜曲率の大きい近視だと,瞳孔は僅か大きい(瞳の大きいほうがキレイに見える ・・・ ?!)
◎瞳孔中心線と照準線
眼球の参照軸には,光軸(optic axis),視線・視軸(visual axis),注視線(fixation axis),照準線(line of sight),瞳孔中心線(pupillary axis)などがある.
解剖学的には眼軸(geometrical axis)というのがあり眼球の前極と後極を通る軸である.これも形状的には角膜頂点が前極,乳頭黄斑間に
後極中心
があるらしいのだが,臨床では(だいたい)照準線上の角膜表面 ⇔ 中心窩(固視点)表面を「眼軸長」としている(この場合,内眼軸).
カメラレンズ系では複数のレンズが組み合わされていても,レンズ光軸は一致するようなっている(共軸光学系).本来の眼は非球面形状で,角膜と水晶体の光軸は一致せず(非共軸;眼の光軸は厳密に規定できないのだそうだ),さらに瞳孔中心は視軸上になく,中心窩も光軸から偏心し,水晶体の屈折率分布も均一ではない.ということで各種の軸が定義され,ややこしい.
光軸:眼球光学系の曲率中心を通る線.中心窩は通らない.
視軸(視線):節点を通り,注視点と網膜中心窩を結ぶ線.ほとんど理論的な定義とのことであるが光軸に対し視軸は鼻側約5° 傾いている(α角).両眼の視軸が交叉する位置が眼前50cm ということで,2Dほど調節して明視する条件が両眼視にとっても球面収差からみても好条件なのだとか.
照準線:注視点と入射瞳の中心を結ぶ.屈折後は射出瞳中心から中心窩に達するとのことで実測され,見ている方向として実用的とされる.
注視線:注視点と回旋点を結ぶ線.回旋点そのものが浮動することで,ほとんど理論的な定義.
瞳孔中心線:計測可能,ということで照準線との“ずれ”角が『λ角』,・・・

このような眼球の特徴をすべて表わした眼球モデルは,現在のところ出来ていない.これを単純化して近似させたのが模型眼である.
◎精密眼・省略眼:Helmholts,Gullstrand,Donders,Listing,Le Grand,などの数値モデル
①省略眼:眼を,ひとつの屈折面(角膜前面曲率)とひとつの屈折率(n=4/3)の眼内媒質とみなして簡素化したもの.調節休止時で代表させている.
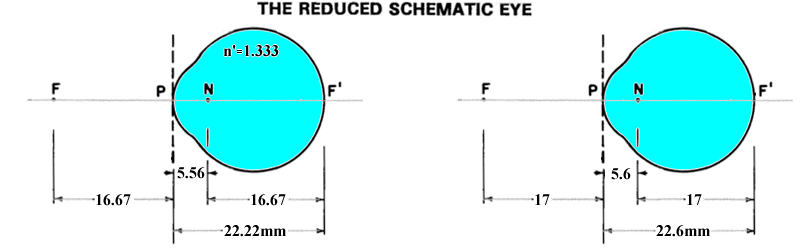
a.眼球を全屈折力を 60D(f=16.67mm),角膜曲率半径は 5.56mm ,この中心を節点,主点を角膜頂点,とするもの.これにより後焦点は 1/60×4/3=22.22mm(Emsley).
b.角膜曲率半径を 5.65mm とする時,全屈折力は D=(4/3-1)/ 0.00565=58.9 .前焦点は 1/D=16.95mm ,後焦点は 16.95+5.65=22.6mm.
c.屈折率 n=1.336 ,主点は 1.5mm(前房内),節点は 7.2mm(水晶体後半),前焦点は 17.2mm,後焦点は 22.9mm,全屈折を 58 D とする(Listing).
d.屈折率 n=1.336 ,角膜曲率を 5.73mm ,主点は 1.35mm(前房内),節点は 7.08mm(水晶体後半),前焦点は 17.054mm(角膜頂点から15.7mm),後焦点は 22.78mm(角膜頂点から24.13mm),全屈折を 58.6 D とする(Gullstrand).
e.Le Grandの略式眼
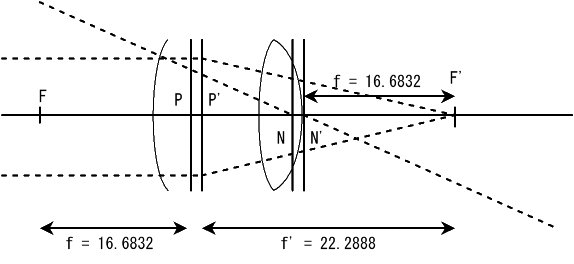
②精密眼
第1主点‐第2主点間距離 0.26mm ,第1焦点(F) 17.055mm ,第2焦点(F') 22.785mm ,節点を第2主点から 5.4mm 0.3mm の位置,角膜頂点は第1主点から 1.35mm の位置,屈折率 1.336(Gullstrand),としたもの.
ちなみに f =f '/1.336
●網膜像は ・・・‥
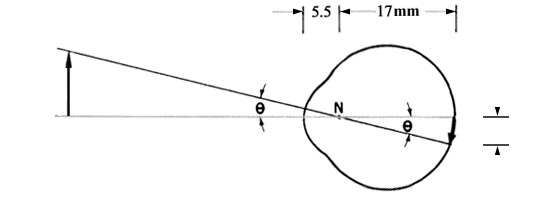
網膜は半径 17mm の円周上にある(眼球の全屈折力を 60D とすると,f =16.67mm ).すなわち,1°≒0.3mm となる.これにより例えば視神経乳頭径は 1.5mm ≒ 5°となる.
視力1.0 の視標は外径視角 5′,ギャップ 1′ということで,網膜にはおよそ 25µm のLandolt環が投影され,1′のギャップはおよそ5µm となる.
半径 17mm の円周として計算すると,5′の弧は 0.0247mm .相似三角形から計算すると 5m(+5.5mm):17mm=7.5:x により,x=0.0254 ...この辺は誤差範囲ということで...

地球 から38万4,400km の距離(光速で 1.3秒)にある直径3,474km の
月
の視角(見込み角)は,およそ0.5°(30分角)となる.これにより眼底像はおよそ 150µm となる.
ちなみに日蝕によると,太陽も見かけの大きさは月と同じと分かる.太陽までの平均距離は約1億5000万km(光速で 500秒)ということで月までの距離の約400倍.これにより太陽の直径は月の約400倍,となる.
では Mariotte盲点の大きさは ? 眼前 33cm の紙面上には,33cm(+5.5mm):17mm=X:1.5 により X=29.6 ということで,あるいは 33cm(+5.5mm)×tan 5°≒29.4 ということで,さらに 33cm(+5.5mm)×tan 15°≒89.9 ということで,
固視点の耳側 9cm で直径 3cm の盲点が検出される(はずである).










