supplement
![]()
は「波」であり「粒」である,ということでしたが,実際には物理特性を論ずるのではなく,進行の仕方さえ理解できれば大丈夫です.
直線性,つまり
・進行を線で表わす,
・方向は左から右へ,
という約束だけです(これが“幾何光学 geometric optics ” です).ここでは,光の特性の一部に触れてみます.
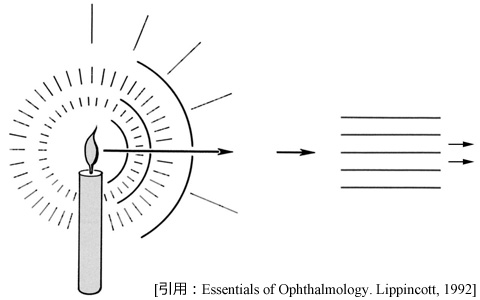
光源から発した光は直進 vergence します ...(アタリマエだ ?
基本的には拡散(放散 divergence )し,これを,
「vergence 」とは,光の広がりの道すじ,ということに置き換えても OK でしょう.かつ,
進行方向を逆にたどると転換できるという共役関係をも意味します.これが,直線性です.
光源から離れると拡散は少なくなり,究極的には「平行光線」となります.平行とは zero vergence です.
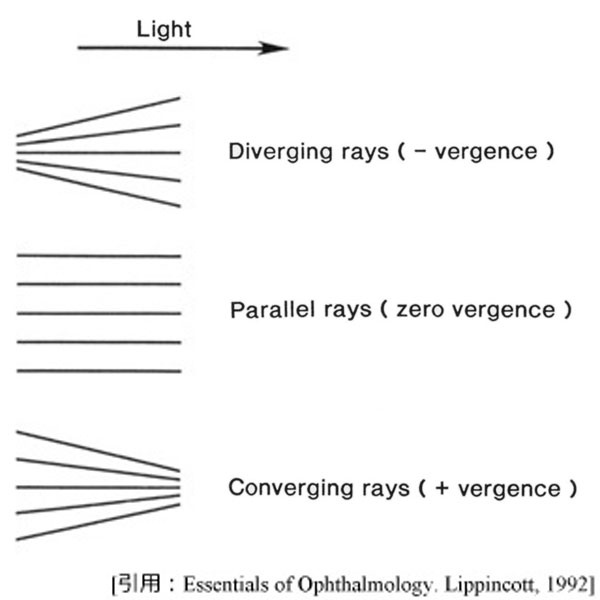
収束(収斂 convergence )する光線は,
vergence の程度を表わす単位が diopter です.発声は(たぶん)「だいおぷた」ですが,日本眼科学会認定の標準用語では「ジオプトリー」といいます.こちらは Dioptrie が元です.
「 D 」と書きます.
光源までの距離を d (単位は m )とすると定義は,
D=1/d (距離の逆数)
従って d =∞ であれば D=0 ということで,平行光線の意味になります.
レンズは光を屈折させ眼球もレンズの作用が必須であることから,「 D 」のお世話になるという訳です.
この
焦点距離をインチ(1 in =25.4 mm)で表わしたものが 度(degree)です.
粒子として :反射・屈折・透過
波動として :干渉・回折・ドップラー効果
眼科では,直線性を考慮した幾何光学 geometric optics の特性が関係します.
a)光は同じ媒質の中で直進し,何かにあたると「反射」します.
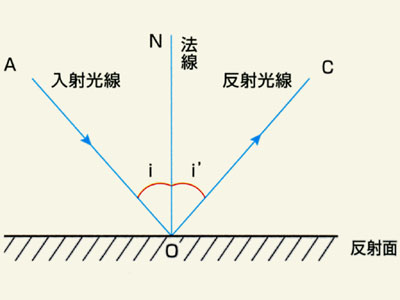
反射:ある角度(i)で入射した光線は,法線(N)に対し反対側に同じ角度(i’)で反射する.
b)透明物体にあたれば透過率に従い「透過」しますが,このとき密度が異なると方向を変えて,新しい媒質の中へ進みます.「屈折」です.
水の入ったコップにさした鉛筆が折れ曲がって見えるのはこのためです.
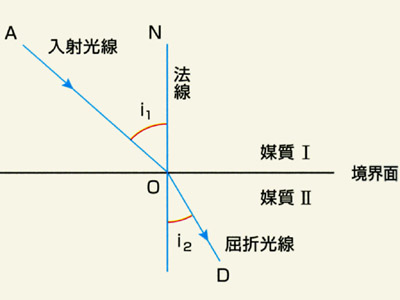
屈折:媒質Ⅰから媒質Ⅱへ透過する光線は,ⅠとⅡの屈折率の比に応じ境界面で方向を変える.
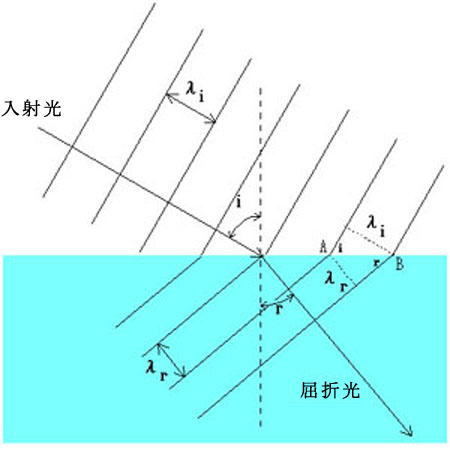
屈折は媒質中での光の速さが異なることから起こる現象です.ふつうにいうと真空中での光速ですが,水中では¾の速度ということが屈折の原理です.因みにダイヤモンドの中では⅖ !
媒質 media:情報伝達の仲介物質,あるいは経路となるもの.
眼では,網膜まで届く光の経路が“optic media”です.この場合,透光体といいます.
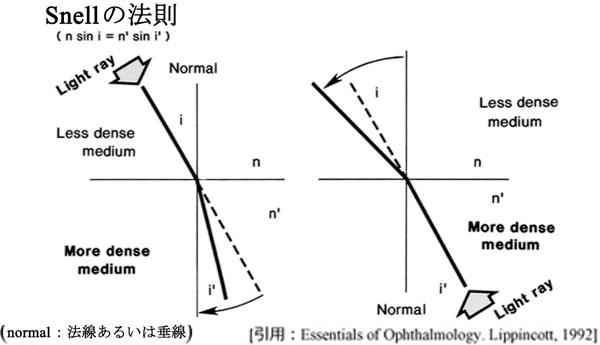
「入射角と屈折角の正弦sin値の比は,二つの媒質内の位相速度(屈折率)の比となる.
あるいは n1sinθ1=n2sinθ2 」 ここで,
n1 は入射側媒質の屈折率,n2 は屈折側のそれ,θ1は入射角,θ2は屈折角.
| 屈 折 率(n)= | 真空中の光速 |
| ────────────────── | |
| 媒質中の光速 |
例えば,角膜は1.376,房水は1.335,水晶体は1.41~3,硝子体は1.335,水は1.333です.
(水はともかく,眼組織の屈折率は模型眼の指定によってわずかに差がある.)
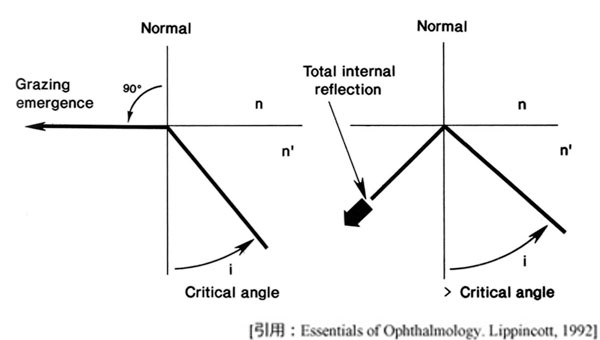
光の経路を逆にするとき入射と同じ経路になりますが,角度 i が臨界角より大であると境界面で全反射し,光は外部に出ません.この原理が光ファイバーです.眼で言うと,眼球を横からどういう角度で眺め回しても虹彩の付け根は見えない.このことは別に触れました.
フェルマーの原理.幾何光学における基礎原理のひとつ.
光は光学的距離が最短になる経路すなわち,進むのにかかる時間が最小になる経路を通る,という原理.これからスネルの法則などの幾何光学の法則が導かれる.直進,反射,屈折の実験事実に基づく法則を示している.
1661年にピエール・ド・フェルマー (Pierre de Fermat ,160?~1665)が発見したそうです.『フェルマーの最終定理』のフェルマーさん,その人です(ちなみに,最終定理を知らなくても視能訓練士の仕事はできます).
光線はレンズの厚みのあるほうに屈折します.
最も単純なレンズのシステムでは
凸レンズは,光軸に平行に入射した平行光線が焦点に収束・結像する.
凹レンズは,光軸に平行に入射した平行光線が焦点から発した光線として拡散する.
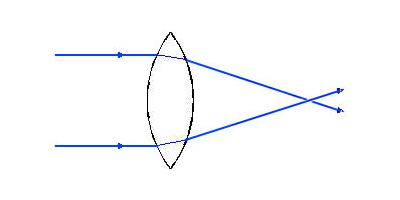
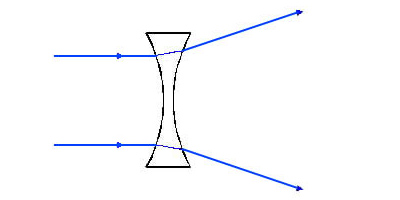
従って,
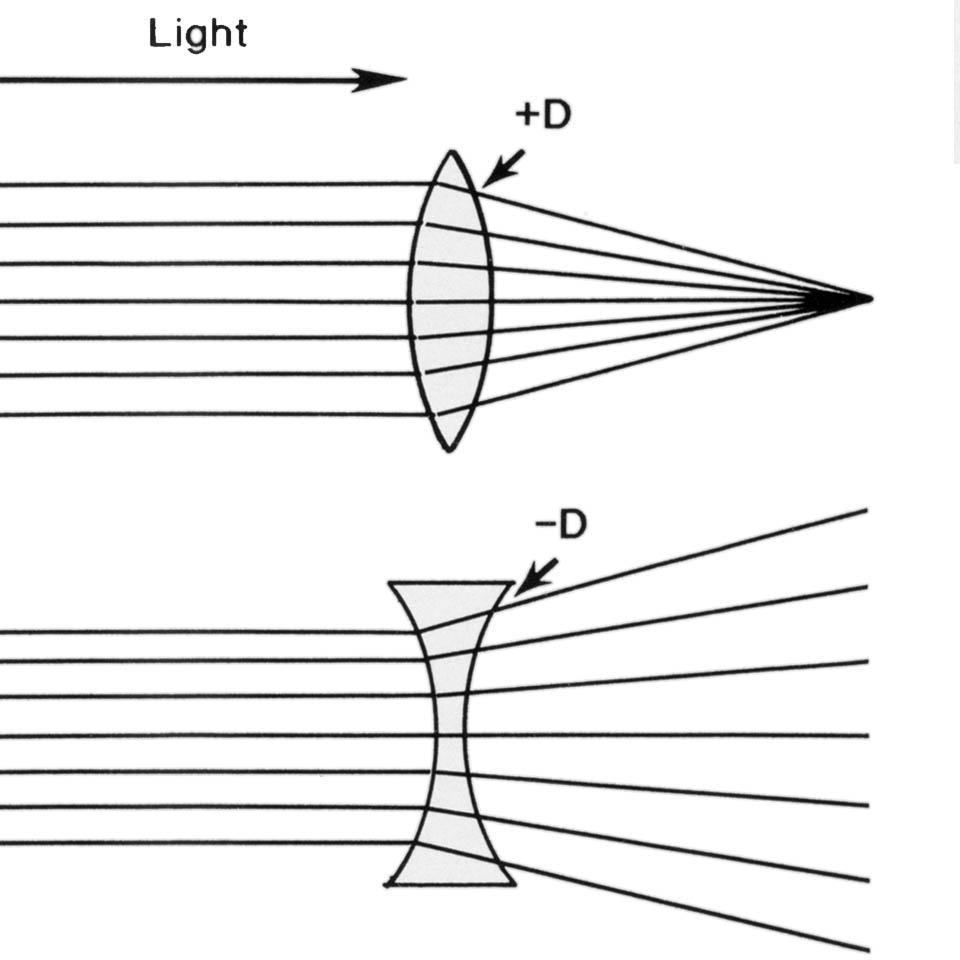
また,
焦点が(光の進行方向に対して)レンズを越えた所(レンズの右側)にある場合を「+」,レンズの左側にある場合を「-」という,
といった説明も可能です.
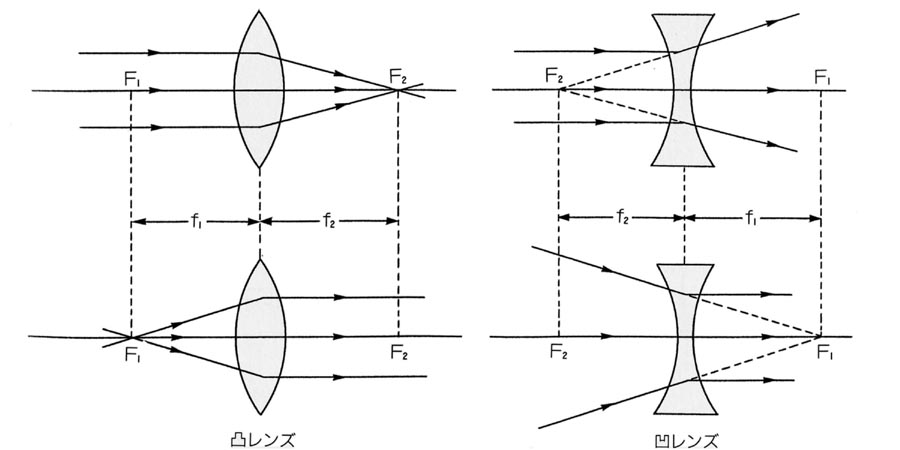
焦点は,光線が通過する光軸上の二か所にあります.
凸レンズは,平行光線を後側焦点(像側焦点)F2 に結像させます,平行光線の進行を逆向きにすると,後側焦点の反対側に前側焦点(物側焦点)F1 が決まります.焦点F1 から出た光線がレンズを通れば平行光線となるわけです.
凹レンズでは,平行光線はレンズの手前の後側焦点(像側焦点)F2 から発した光線として拡散し,レンズの後ろの前側焦点(物側焦点)F1 に向かって収斂する光線はレンズを通れば平行光線となります.
レンズの前後で媒質の屈折率が等しいとき,それぞれのFまでの距離は f1 =f2 で,単に「焦点」と言うと,F2 すなわち後側焦点を指します.
そんな訳で「+」レンズは焦点がレンズを超えたところにあり,「-」レンズの焦点はレンズの手前にあることになります.
レンズの強弱とは vergence の程度ですから,単位は「D」です.
この場合,焦点距離 f(単位 m )に対して,
| D= | 1 | (焦点距離の逆数) |
| ―― | ||
| f |
度のないレンズを仮定すれば,D=0 すなわち, f=∞ であります.
レンズ(あるいは眼科では「屈折」・・・重要ですゾ)の世界では,「D」で加減(+-)の計算をします.
例えば,
焦点距離 1 m の凸レンズは 「+1D」,
焦点距離50cm の凹レンズは「-2D」です.
では,この二つのレンズを重ねるとどうなるでしょうか(レンズの厚みは無視することとする).
結果は「-1D」となります.単純な計算でOKです.
難しく言うと,光線の経路は入射する vergence(U)と通過後の(レンズの「度(P)」による) vergence で焦点(V)が決まる,
となります(レンズとは光線の経路を変換changeするもの,ということ).
U+P=V
U(ジオプトリ)=レンズに当たった時の物体の光の広がり(object vergence),
P(ジオプトリ)=レンズの屈折力(vergence ‐ change),
V(ジオプトリ)=結像点での光の広がり(image vergence),
通常,レンズといえばこれです.模型的には平面で書かれる断面図も,現実には立体のレンズですネ.この場合
これを 球面レンズ といいます.
断面は 180°回転させると天地が重なります(181°=1°).
この反時計周りの 180°の概念は重要です.
レンズを細かく分割しても個々それぞれのレンズは同一の焦点になっています(収差は無視する).小さいレンズの集合とも言い換えられます.レンズを半分(半月状)にしたとき,視野の半分しか映らないわけではなく,明るさが半分になるだけです.
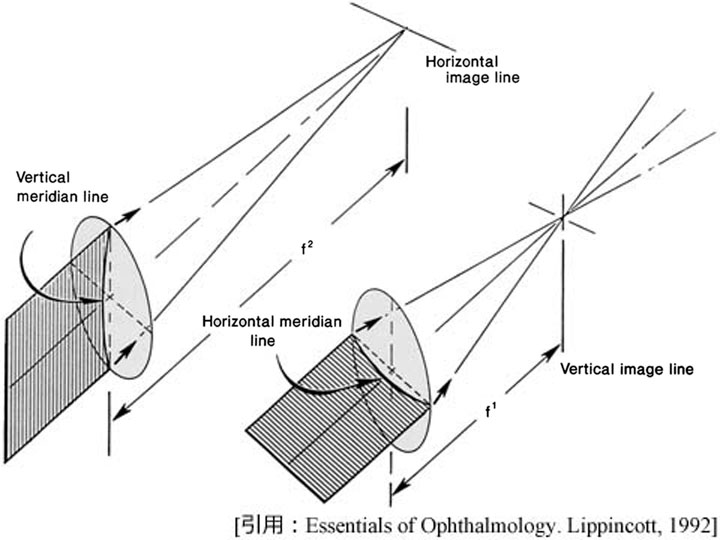
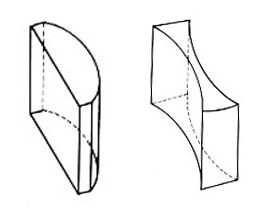 ところが実際には,レンズ断面の角度(経線 meridian )によって焦点距離が変わる屈折系があります.
ところが実際には,レンズ断面の角度(経線 meridian )によって焦点距離が変わる屈折系があります.
「眼」です.
例えば水平断での焦点の位置と垂直断でのそれとは一致しない,というような場合です(乱視のことですが病気ではありません・・・・念のため).
先ほど上で,複数レンズの度数の合成に触れました.「眼」を合成レンズと考えて球面レンズ分を引く,たとえば垂直経線方向の度数を「0」にすると,水平経線方向に残余度があるわけです.
これを 円柱レンズ といいます.
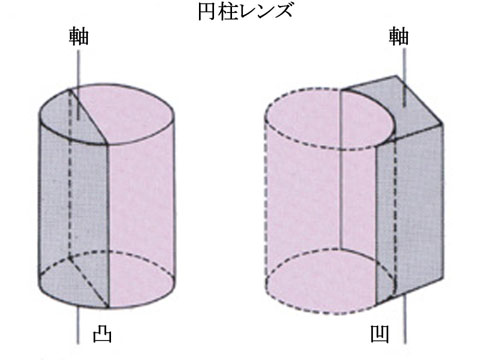
円柱レンズ とは円柱を縦に切り取った形のレンズです.
ここの模型図では,横から見ると断面(垂直方向)は長方形となっており,屈折力がありません.上から見ると断面(水平方向)は「凸」か「凹」の形で屈折力のあることがわかります.
屈折力の無い方向を「軸 axis 」と言います.
軸と直角方向に屈折力が有ります.
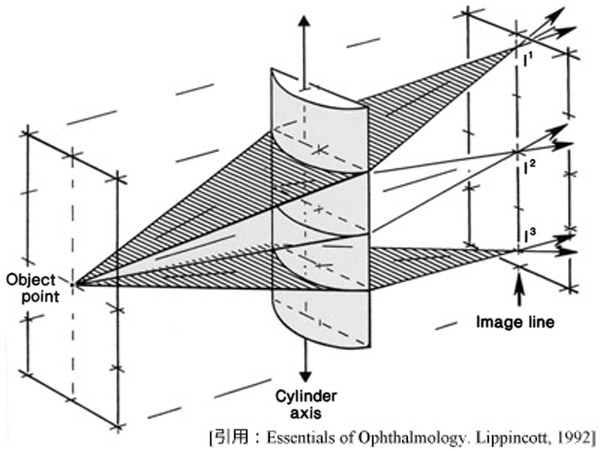
物点の結像は一点にはならず,線になります.「焦線 image line」です.
線の方向が「軸 cylinder axis」です.これが臨床で使う「乱視軸」です.
球面レンズと円柱レンズの組み合わせで,互いに直交する2つの屈折力で作動します. 眼鏡レンズの時代では,あまり使われることがなかった「トーリック」ですが, 乱視矯正コンタクトレンズ,さらに眼内レンズが一般化して「トーリック」が謳われるようになりました. やっぱり,カタカナの魅力ですかね.
ベーシックなレンズ系について,以下に補足する.
もう少し
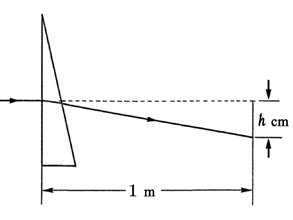
●プリズム屈折力 prism power:
プリズムから1m 離れた所で h cm の直線偏移を生じるプリズムによる光線の偏角能力.
単位はプリズムジオプトリー(⊿).
1⊿ は約0.57°,10⊿ は約5.71°,20⊿ は約11.3°・・・・
●レンズの物体面(O)・ 像面(I)
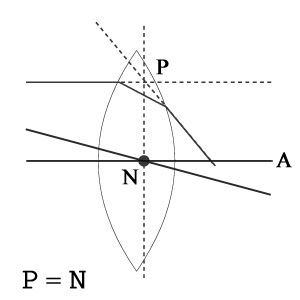
屈折は屈折率の異なる媒質の境界面で発生する.すなわち入射光線はレンズ表面で一度屈折し,レンズ裏面で再度屈折し射出することになる.
光線追跡により,入射光をそのまま延長した線と射出光が出てきた元の方向に戻る線は,右図Pにて交わる.この交点を含む光軸に直行する平面を想定したものが主平面である.表現を変えれば,入射光はこの主平面で折れ曲がって焦点に向かう.主平面と光軸との交点が主点である
焦点距離はここを基準として測る.
レンズ面に対して垂直であり,光軸線は進行方向を変えられることなく直進する.この光線が当たるレンズ上の位置が軸上点である.
軸上点を通るすべての光線は,屈折せずに直進する.「節点」である.
光学系への入射角と出射角が常に等しい点(つまり直進する).「結点」.
通常の光学系は物体側と像側の媒質とも空気であるので,多くの場合「節点」と「主点」は一致する.
眼では物体側が空気であるのに対し像側が硝子体であるため,両者は一致しない.
●レンズによる像(薄い単レンズ)その1
レンズ通過後の光線が収束して一点に集まる場合は実像,光線が発散して逆向きに延長した光線が一点を通る場合は虚像である.物体と像の上下が同じ場合を正立,逆の場合を倒立という.
光線が一点(物点)から出てレンズを通った後,他の一点(像点)に集まるとき,逆に後者から出た光は前者に集まる.この2点を共役点という.
●レンズによる像(薄い単レンズ)その2
レンズから有限の位置にある物点Oの像Iは,
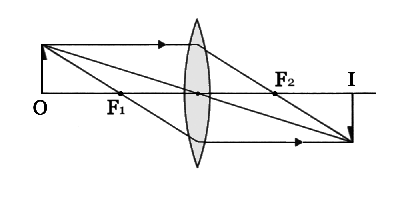
①前側焦点(F1)を通る光線はレンズを通過後,光軸に平行に進む,
②光軸に平行な光線はレンズを通過後,後側焦点(F2)を通る,
③レンズの中心に向かう光線は,そのまま直進する,
これらにより,三本の直線により作図する.
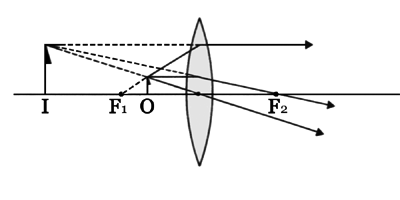
| 凸レンズでは, | |
 |
 |
| 凹レンズでは, | |
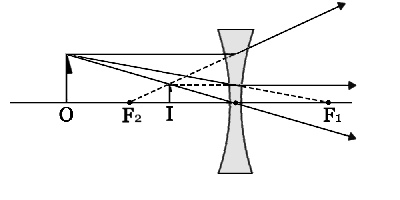 |
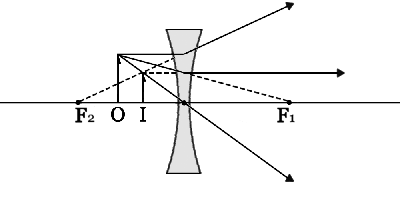 |
さらに
◎拡大・縮小の考え方は,大きく3種類ある(ようだ ? ・・ ✔ 各自
調べてください ).
①レンズの結像を作図・計算
②拡大鏡としての distance magnification
③眼鏡レンズとしての spactacle magnification
である.
since 2004@視能矯正
![]()