■視力の概念
形態覚(形態神).3次元的に広がる物の形や存在を認識する視能力の鋭敏さ.
最小分離閾はその基本である.
■形態覚
視力 とは2点を2点と認識できる機能である.2点間の開きを 角度(見込角)で表わし,その認識限界 minimum angle of resolution(MAR)が分解能,すなわち鋭敏さ acuityである.見込角visual angleは眼科用語では 視角 という.
臨床では,視力の単位を視角1分(1′)とする.
①最小分離閾 minimum resolvable (separable):
視標の形がわかる,あるいは2つの点を2つとして分離する閾値.1′≒0.0167 degrees.
②最小可読閾 minimum legible:
文字試視力表で評価しているもの.文字を判読できるかどうか.
③最小視認閾 minimum visible (cognostible or perceptible):
視標(目標)の有無の認識,1線または1点を認める閾値.たとえば,ケシ粒より小さい点々,はるか遠方の飛行物体,星のひとつひとつ.0.5″≒0.00014 degrees.
④副尺視力あるいは最小識別閾 vernier acuity or minimum discriminable:
2本の線分が連続した1線であるか,ずれているかを感知するもの.分解能ではなく位置や大きさの弁別能をみているのだとか.分離閾より3〜10倍感度が良い(超視力 hyper acuity)が,教科書によっては1″以上あるとするものも.
網膜中心窩において個々の錐体サイズは,2µm(0.4′ あるいは24″)乃至 2.5µm(0.5′ あるいは30″)程である,ということが分解能の限界を説明するひとつの条件になっている.
ギャップを認識するための中心⇔中心により,前者では少数視力1.2,後者では1.0に相当するということになる.
(詳しい話は 視能生理学の講義を !)
★不確定要素:視標の形状,周囲の明るさやコントラスト,網膜の順応状態,瞳孔径,視標の提示時間 ・・・・
視標の形状
実際に使われる「視力」測定では“最小分離域を基本概念として,最小可読域を用いて実用上差し支えない”,と解釈されている(1909,国際眼科学会).
明るさとの関係
視力は視標の輝度が大きくなるほど良好になる.ただし網膜の順応状態も暗順応から明順応へ変化する.
順応との関係
明順応状態では,視標の明るさが網膜が順応している明るさに近い時最高の視力が得られる.
コントラストとの関係
100%コントラスト時の視力に比べ,40%のコントラスト時では8割ほど,20%コントラストでは7割ほどに低下する.
(通常の視力検査視標は白地に黒字であることで,100%コントラストとなる.
より広範な視能力を評価する手法では周波数特性による視能力の表示がある.視覚系の周波数特性は,❶空間周波数特性 と ❷時間周波数特性 で表わされる.ある瞬間の入力情報についての情報処理が空間周波数特性となり,時間的変化に対する出力の情報処理が時間周波数特性となる.
入力波形を正弦波の和に分割し(Fourier 変換),多数の正弦波に対する応答の総和で出力レスポンスを知る.正弦波の入力・出力の振幅比・位相ずれで伝送系の機能を表わす.
【 ☞ 続きはこちら 】
★両眼視による視力の加算 binocular summation:感度や信号対雑音(SN比)の改善は,単眼視
の √2 倍となる.
0.15 log unit  LECTURE NOTES (外部リンク)
LECTURE NOTES (外部リンク)
■視力の単位
視力 visual acuity の検定には,Landolt環 を視標として使う.Cマークの切れ目が見えるかどうかはそれなりにファジーなものといえようが,それはともかく,見かけの視標の大きさは距離で変わってしまう.これでは不便なため切れ目(2点間の幅)を角度angleで表わし,この「視角 visual angle 」を用いることで視標までの測定距離の条件が消えることになる.
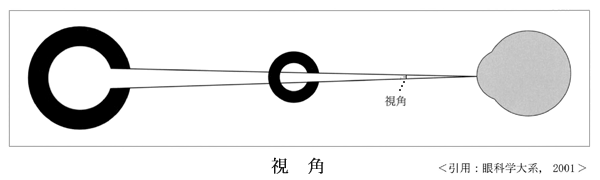
〖視角を作る中心は節点(第一節点:角膜の後方 5.5mm .あるいは網膜面から 17mm )〗
【☞ この辺は
生理光学 の講義で 】

⓪標準視力 standard
視力=視角の逆数 と定義している.
最小分離域で表す視力の基準は視角1′ である.これを分離(隙間を認識)できたときが,視力1.0 となる.つまり 視力 と 視角 は同義である.また視角1′ の視標が「標準Landolt環」である.
視力1.0用のLandolt環は1.5 mm ということであるが,これを作図しようとすると,1′ は1.45 mm 余りの計算になる.なにせ外径7.5 mm である.3%の誤差は許してあげよう.
さて,視力の元は視角,ということで角度の目盛を付けようとすると 0 1 2 3 ..となるのが自然,といえる.60進法でも10等分で ~ 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 ~ と表記できる.何を言いたいのだ ?
①小数視力 decimal
視角1′ に対する視力が1.0,10′ では0.1 となる.通常の試視力表は,視力値0.1の等差で作られている.
ここで,2′ では0.5,5′ では0.2 であるので,0.1 ⇔ 0.2 では倍または半分の関係にあり,同様に視力1.0 の半分では0.5 が対応する.小数視力では,0.2 から一段階の低下は「0.1」であり,1.0 から一段階の低下は「0.9」となる.
すなわち試視力表の,例えば0.2 ⇔0.1 と1.0 ⇔0.9 での一段階は,比例になっていないとわかる.その所為か,
国際眼科学会(1909)のお墨付のはずのLandolt環と小数視力は,なぜか肩身が狭い.分数視力に気を使いすぎるような気がする.
②対数視力 logarithm
小数視力と互換性があり本質的に変わるものではない.視角の対数値により,視力の変動を定量的に表現すること,平均視力の計算が容易となること,等が可能.
ⓐ 小数視力をグラフにするとき,0.1 ⇔ 0.2 ⇔ 0.4 ⇔ 0.8 ⇔ 1.6 のように対数間隔にすることがある.
対数値に変換すると
| 小数視力 1.6 | では | log10 1.6 | ≒+0.2 , |
| 小数視力 1.0 | では | log10 1 | = 0.0 , |
| 小数視力 0.8 | では | log10 0.8 | ≒-0.1 , |
| 小数視力 0.4 | では | log10 0.4 | ≒-0.4 , |
| 小数視力 0.2 | では | log10 0.2 | ≒-0.7 , |
| 小数視力 0.1 | では | log10 0.1 | =-1.0 |
...... となる. |
これにより,0.1 ⇔ 0.2 ⇔ 0.4 ⇔ 0.8 ⇔ 1.6 は対数値で 0.3 の等間隔と分かる.
根本的には「視角」を用いた対数表記が「logMAR 値」である.
ⓑ 視角を常用対数で表わしたものを「logMAR 値」( logarithm of Minimum Angle of Resolution )という.
視角を等間隔で表示したものとなる.
| 視角 1′ (小数視力 1.0) | では | log10 1 | = 0.0 , |
| 視角 2′ (小数視力 0.5) | では | log10 2 | ≒+0.301 , |
| 視角 3′ (小数視力 0.33) | では | log10 3 | ≒+0.477 , |
| 視角 4′ (小数視力 0.25) | では | log10 4 | ≒+0.602 , |
| 視覚 5′ (少数視力 0.2) | では | log10 5 | ≒+0.699 , |
| 〜 | |
| 視覚10′ (小数視力 0.1) | では | log10 10 | =+1.0 |
...... となる. |
小数視力1.5 に相当する視角を0.667′ とすると log 0.667 ≒ -0.176 ,
小数視力2.0 では log 0.5 ≒ -0.301 .
そこで例えば,
視角 1′ (小数視力 1.0)⇔視角 0.67′ (小数視力 1.5)の差(logMAR 値 0.0 ⇔ -0.176)と
視角 3′ (小数視力 0.33)⇔視角 2′ (小数視力 0.5)の差(logMAR 値 +0.477 ⇔ +0.301)が同じ「0.176」
となっている.つまりそれぞれ
2/3の大きさの関係となる.
視角 0.67′ (小数視力 1.5)⇔視角 0.5′ (小数視力 2.0)の差(logMAR 値logMAR 値 -0.176 ⇔ -0.301 )と
視角 4′ (小数視力 0.25)⇔視角 3′ (小数視力 0.33)の差(logMAR 値 +0.602 ⇔ +0.477 )も同じ「0.125」,すなわち
3/4の大きさの関係となる.
視角 10′ (小数視力 0.1)⇔視角 5′ (小数視力 0.2)の差と視角 3.33′ (小数視力 0.3)⇔視角 1.67′ (小数視力 0.6)の差も言うまでもない(計算してみてください).
少々桁数が煩雑となってくるので,近似値で評価すると,
| 小数視力 | ⇔ | 視 角 | ⇔ | logMAR値 |
| 0.05 | ・・・・ | 20 ′ | ・・・・ | +1.3 |
| 0.1 | ・・・・ | 10 ′ | ・・・・ | +1.0 |
| 0.13 | ・・・・ | 8 ′ | ・・・・ | +0.9 |
| 0.16 | ・・・・ | 6.31 ′ | ・・・・ | +0.8 |
| 0.17 | ・・・・ | 6 ′ | ・・・・ | +0.78 |
| 0.2 | ・・・・ | 5.0 ′ | ・・・・ | +0.7 |
| 0.25 | ・・・・ | 4 ′ | ・・・・ | +0.6 |
| 0.3 | ・・・・ | 3.33 ′ | ・・・・ | +0.52 |
| 0.32 | ・・・・ | 3 ′ | ・・・・ | +0.5 |
| 0.4 | ・・・・ | 2.5 ′ | ・・・・ | +0.4 |
| 0.5 | ・・・・ | 2.0 ′ | ・・・・ | +0.3 |
| 0.56 | ・・・・ | 1.8 ′ | ・・・・ | +0.26 |
| 0.6 | ・・・・ | 1.67 ′ | ・・・・ | +0.22 |
| 0.63 | ・・・・ | 1.6 ′ | ・・・・ | +0.2 |
| 0.7 | ・・・・ | 1.43 ′ | ・・・・ | +0.16 |
| 0.71 | ・・・・ | 1.4 ′ | ・・・・ | +0.15 |
| 0.8 | ・・・・ | 1.25 ′ | ・・・・ | +0.1 |
| 0.83 | ・・・・ | 1.2 ′ | ・・・・ | +0.08 |
| 0.9 | ・・・・ | 1.11 ′ | ・・・・ | +0.05 |
| 1.0 | ・・・・ | 1.0 ′ | ・・・・ | 0.0 |
| 1.26 | ・・・・ | 0.79 ′ | ・・・・ | -0.1 |
| 1.58 | ・・・・ | 0.63 ′ | ・・・・ | -0.2 |
| 2.0 | ・・・・ | 0.5 ′ | ・・・・ | -0.3 |
| と,なる. |
|---|
肝腎の「logMAR 値」でいうと,logMAR 0 は視角1′(小数視力 1.0)ということで,
logMAR値 0 = 視角 1.0′ ;小数視力 1.0
logMAR +0.1≒ 視角 1.259′;小数視力 0.7943
logMAR +0.2≒ 視角 1.585′;小数視力 0.6310
logMAR +0.3≒ 視角 1.995′;小数視力 0.5012
logMAR +0.4≒ 視角 2.512′;小数視力 0.3981
logMAR +0.6≒ 視角 3.980′;小数視力 0.2512
・・ 〜
logMAR +1.0= 視角 10′ ; 小数視力 0.1
ここでは,1.259×1.259≒1.585,1.585×1.259≒1.995,1.995×1.259≒2.512,・・・ すなわち,
logMAR で 0.1 の差とは 約1.25倍(100.1=1.2589254・・・・・ , log1.25892=0.1)ずつの比となっていることで,小数視力では 1.0⇔0.8/0.5⇔0.4/0.1⇔0.08 などの差と同じことになる.
また,2倍(あるいは半分)とは logMAR で 0.3 の差(3段階)ということで,1.0⇔0.5/0.8⇔0.4/0.6⇔0.3/0.4⇔0.2/0.2⇔0.1 などの差を表わしている.等比配列というわけである.これらにより,例えば
logMAR値 0.2 と 0.4 の算術平均 0.3 において,
視角では幾何平均√(1.585×2.512)=1.995 と一致する.小数視力相当では 0.63 と 0.4 との平均が 0.5 ということになる.
対数を使う意味は,「感覚の大きさは,刺激の大きさの対数に比例する(Weber-Fechnerの法則)」ことから.これでいくと,
従来のスタイルでの視力検査の出発点は 小数視力0.1 であるから次は 0.2 として,0.4,0.8,1.6,3.2 と続かなければならない.同じように健常小数視力1.0 から半分に減退した状態では 0.5,さらに 0.25,0.125,0.06 という間隔で評価しなければならない.しかし,
視力が「0.0」になったり,表記に「+」や「-」が付く感覚は別として,要するに,どこで使う のか って ???
③分数視力 fraction
以上の視力検査は,わが国では 5 m で検査するように視標の大きさを決めている.
アメリカやヨーロッパのいくつかの国では,20 feet(あるいは 6m )で検査し,視標は,視角1′ となる時の距離の号数がつけられている.視力は,検査距離/号数で表記する.
すなわち,20 feet 距離での視角1′ は 1.75 mm(20号),15 feet( 4.5m )では 1.31 mm(15号),・・・
25 feet( 7.5m )距離では 2.18 mm(25号),100 feet( 30m )では 8.72 mm(100号),・・・
そうして,20 feet 視標(20号)が読めた時 「20∕20」 と表わす.15 feet 用の視標が(20 feetで)読めれば 「20∕15」 となる.
同様にして,100 feet 用視標が( 20 feet で)ようやく読めた時は 「20∕100」 である.
これらはそのまま,「20∕15 = 1.33」 「20∕20 = 1.0」 「20∕100 = 0.2」 と ・・・
ページ始に戻る
■ 1 ′ (いっぷん)とは ?
角度と時間は,60進法と12進法を用いて組み立てられている.
角度は,度(degree,°)=円周を360等分した弧の中心に対する角度あるいは π∕180ラジアン,分(minute,′ )=度の60分の1,秒(second,″ )=度の3600分の1 である.
地図の経度・緯度も同じで,ちなみに現地(帝京大学のこと)は東経139度43分5秒,北緯35度45分24秒.
時間は,1日=24時間(12時間×2),1時間=60分 ,1分=60秒ということだが,そもそも1日の長さ自体が微妙に変動しているとかで,現在ではまず
秒が定義 されていることは周知のとおり.すなわち,
セシウム133原子の特性を利用して1秒を決定,秒の60倍を分(minute,′ ),秒の3600倍が時(hour, ° ).
時間と角度の接点は,月が30日の周期で12回朔望する=1年=360日=太陽が黄道上を1周する,ということ.この辺はメソポタミアだかバビロニアあたりまでさかのぼるそうだ.興味と時間があれば調べてみたらどうでしょう.
ともかく,12という数字は大きな意味があったそうである.
余談,その 1 .ということで,おお昔のひとは空に720個の太陽を並べると一周りすることに気づいていた.ということで,天空に見える太陽の大きさ(見込み角)は30′(0.5°)となる.
余談,その 2 .分 の単位記号は『 ′』で『プライム』という.秒の記号は『 ″』で『ダブルプライム』という.60進法の慣習で,ある単位(たとえば
1 時間)の60分の1 を“prime minute”,さらに60分の1 を“second minute”,さらに60分の1 を“third minute”の様に表現し,これに対応して
数の右肩に点( ′)を 1 つ,2 つと打つ表記がされるようになった,とのことである(wikipediaによる).minutes や seconds はここから出来たのかな ?
要するに記号(約物)としては『 ’』や『 ”』とは別物なんだそうである(フォントによるデザインの違いは触れないことにする).
余談,その 3 .長さの基準はメートル(metre).光(波長は 1 mm 〜 2 nm 程度の範囲)は波長域によって赤外線・可視光線・紫外線に分けられ,より長い波長のラジオテレビ放送の電波(ラジオ波)とかさらに短い波長の放射線(X線,など)と同列の電磁波(視能学第2版 84ページ)である.電磁波の真空中での伝搬速度は299,792,458m 毎秒ということである.これにより,1メートルとは真空中で1秒の2億9979万2458分の1 の時間に光が進む長さ,となっている.
元の1メートルの定義は北極点から赤道までの(子午線)距離の1000万分の1.そうすると地球の外周は4万kmということで,光の速度(≒30万km毎秒)では1秒間で7.5周ということになる.地球から月までの距離は38万4400kmということで光速で1.3秒,太陽までの距離は1億5000万kmということで光速で8分20秒.
余談,その 4 .放送電波では一般には周波数を使う.例えばラジオではNHK東京第一放送(JOAK)は 594kHz,NHK東京FM放送(JOAK-FM)は 82.5MHz,など.電波と呼ぶ上限はテラヘルツ波の 3THzで,これ以上は赤外線の領域とかで波長を使う.赤外線は 1 mm(=1000µm) 〜 0.7 µmに分布する.可視光線は 0.7 µm(=700 nm) 〜 400 nm,紫外線は 400 nm 〜 1 nm となる.
また 750nm波は 400THz,3 THzでは波長 900µm,UHF 13チャンネルでは 473MHzとして波長 63cm,82.5MHzだと波長 3.6m,となる.短波放送では何何メーターバンドとか言う.
因みに以前 光の波長は10-10メートルを定義とする【Å】(おんぐすとろーむ)という単位で表していた.
| 1 dm | (デシメートル)粉 | =10-1m | ;10分の1メートル |
| 1 cm | (センチメートル)糎 | =10-2m | ;100分の1メートル |
| 1 mm | (ミリメートル)粍 | =10-3m | ;1000分の1メートル |
| 1 µm | (マイクロメートル)粆 | =10-6m | ;100万分の1メートル |
| 1 nm | (ナノメートル) | =10-9m | ;10億分の1メートル |
■ 視標 : Landolt と Snellen
基準は,外周 5′,内周 3′(すなわち,輪の太さ 1′),ギャップの1辺 1′ となっている Landolt 視標である.
国際的な取り決め(1909)での「1.0 Landolt 環」は,5m 測定で 1′ を 1.5mm としたものである.
Landolt 環の説明に,「7.5 mm の直径,太さ 1.5 mm,ギャップ 1.5 mm四方」とある教科書が多いが,作図不可能ではないか(上図・左)? どーするの ?
■ JISがあるさ
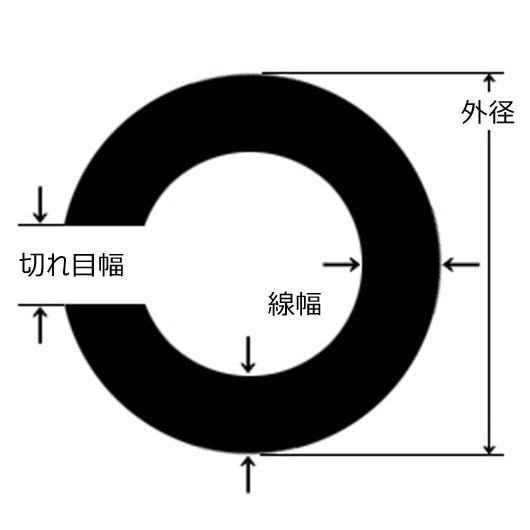
JISには,
『ランドルト環視標の寸法は,視力値 1.0 のランドルト環の外径を視覚 5′ ,線幅および切れ目幅を視覚 1′ とし,視力値 a の視標の寸法は,視力値 1.0 の視標の
1∕a とする.』
とあります.心配無用というか,切れ目部分の線幅(1.03倍になるとか)には言及してません.手元の教科書を確認しましょう.
■ 視力とlogMARの付け足し
眼の分解能は臨床的には視力で評価されるが,視力は眼球光学系の結像特性だけでなく視標の性質や提示条件,光そのものの特性,さらには網膜の順応状態や網膜から中枢までの情報処理系の特性や心理的要因によっても影響を受けるため,視力概念そのものに曖昧さがつきまとうことになる.
視力の表現は,従来から臨床現場で多用されてきた通常の小数視力や分数視力(メートル系とフィート系)ではそのスケールが等間隔ではないことから,種々の問題が残る.一方,対数視力やlogMARは等間隔スケールとなり,統計処理で有利である.
なお,logMARを対数視力のようにlogMAR視力と表現するのは誤りである.logMARは最小視角の対数値であり,明らかに視力ではない.小数視力に慣れている我が国では,logMAR値と小数視力換算値を併記するなどの工夫が推奨されている.例えば,術前logMAR値1.0(換算小数視力0.1)から術後logMAR値0.0(換算小数視力1.0)などである.
魚里氏は「決してlogMAR視力1.0のような表現は避けてください。logMARそのものは視力ではありませんので、logMAR値の表現の方が望ましいでしょう。」と述べている.
一応,1.0logMARとか0.7logMARという表現は許容されている.
■ 診療録での記載
カルテでは,
*右眼視力:Right VA,RV,Vd(visus dexter)
*左眼視力
■ 小数視力0.1以下のlogMAR値の付け足し
| 小数視力 | ⇔ | 視角 | ⇔ | logMAR値 |
| null | ・・・・ |
lim
log X
| ・・・・ | ∞ |
| 0.003 | ・・・・ | 330′ | ・・・・ | +2.5 |
| 0.004 | ・・・・ | 250′ | ・・・・ | +2.4 |
| 0.005(25cm指数相当) | ・・・・ | 200′ | ・・・・ | +2.3 |
| 0.006 | ・・・・ | 166′ | ・・・・ | +2.2 |
| 0.008 | ・・・・ | 125′ | ・・・・ | +2.1 |
| 0.01 | ・・・・ | 100′ | ・・・・ | +2.0 |
| 0.0125 | ・・・・ | 80′ | ・・・・ | +1.9 |
| 0.16 | ・・・・ | 63.1′ | ・・・・ | +1.8 |
| 0.02 | ・・・・ | 50′ | ・・・・ | +1.7 |
| 0.025 | ・・・・ | 40′ | ・・・・ | +1.6 |
| 0.03 | ・・・・ | 33.3′ | ・・・・ | +1.52 |
| 0.032 | ・・・・ | 31.6′ | ・・・・ | +1.5 |
| 0.04 | ・・・・ | 25′ | ・・・・ | +1.4 |
| 0.05 | ・・・・ | 20′ | ・・・・ | +1.3 |
| 0.06 | ・・・・ | 16.7’ | ・・・・ | +1.22 |
| 0.063 | ・・・・ | 15.8′ | ・・・・ | +1.2 |
| 0.07 | ・・・・ | 14.3′ | ・・・・ | +1.16 |
| 0.08 | ・・・・ | 12.5′ | ・・・・ | +1.1 |
| 0.09 | ・・・・ | 11.1′ | ・・・・ | +1.05 |
| 0.1 | ・・・・ | 10′ | ・・・・ | +1.0 |
| 0.2 | ・・・・ | 5′ | ・・・・ | +0.7 |
こうしてみると,例えば 0.09 などはあまり意味がないようである(患者へのムンテラには大事なのだが).しかし 0.01 ⇔ 0.02 などは,やけに細かい.そうです,low vision 側に優しいのです.でも,この辺の視力って,どうなのかなあ ? ?
■ ETDRSチャートの付け足し
ETDRS(Early Treatment Diabetic Retinopathy Study)チャートは従来の視力表に比べ低視力者におけるわずかな視力変化を検出できる方法で,主に臨床試験で使用されている.10字多く見えれば2段階,15字多く見えれば3段階の視力改善といえる.
視標は可読文字ということでMARではないが,文字間と列間が対数スケールであることで,1文字あたり0.02log単位で計算しlog値としてスコア化する.


たとえばlogスコア+0.2(少数視力0.63)ラインを5文字クリアして,次の列(logスコア+0.1,少数視力0.8)が1文字読めれば0.18,2文字で0.16,次は0.14,0.12ということで,5文字クリアして0.1とスコアする.倍あるいは半分はlog値0.3であるから,3ラインまたは15文字に相当する.
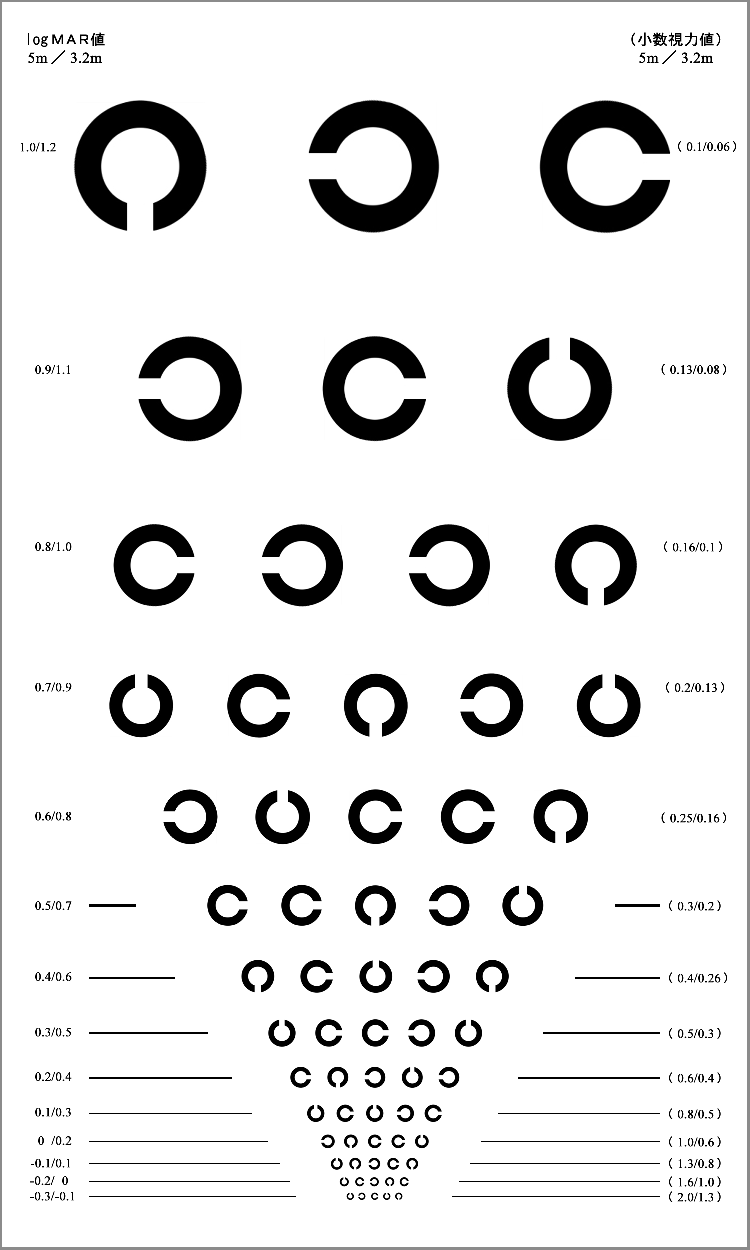
■【logMAR視力表】
視標の間隔と列間が対数スケール,というのがミソ らしい(石原式試視力表との違い).
![]() LECTURE NOTES (外部リンク)
LECTURE NOTES (外部リンク)






